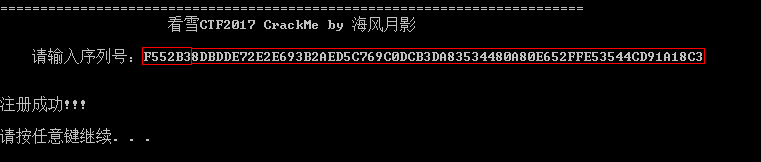
正在下载:crackme-rsa.zip 看雪CTF2017学习记录整理系列5

跟着引用进去便能直接定位到赤裸裸的一个主函数,F5稍加分析一下流程,判断了输入key为70位字符:

判断完了输入长度后还检查了输入字符是否在大写的十六进制字符集里,并且将其分为前6位和后64位两个字符串,分别对应两个16进制“大数”:

接着就能看到上面“查看字符串”里的两个大数串,分别参与到程序运算和比较中去,最后判断是否符合预期:
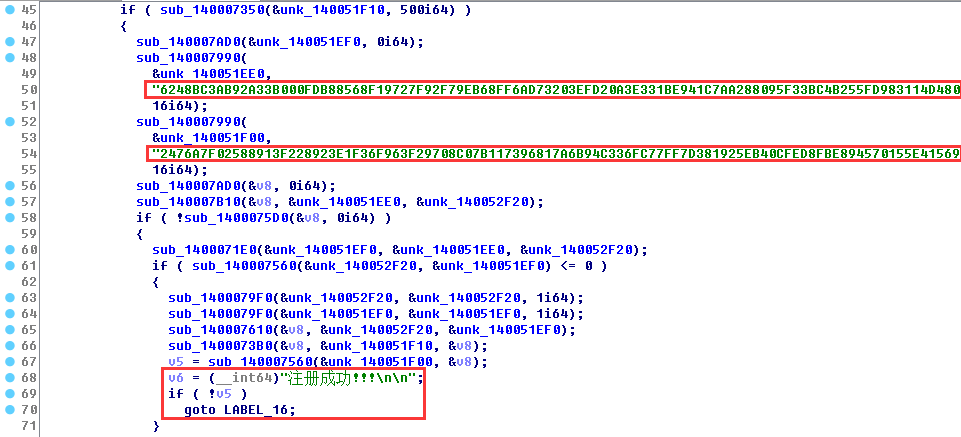
也就是说,我们只需要搞清楚这些运算的流程与含义,最后进行验证就可以了,逻辑一目了然比较清晰。关键就是这里面不多的几个运算函数,如果你进去细跟的话基本就调入坑里了,实际上它们都是一些第三方的调用库编译出来的,这个怎么看呢?还是字符串:
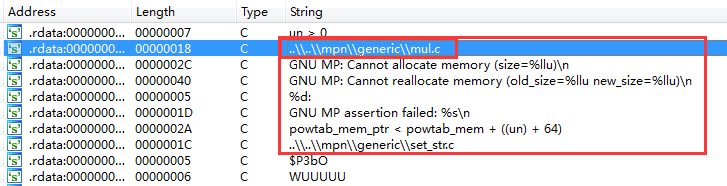
随便搜索引擎都能知道这是个出名的数学运算库:
找到其官网https://gmplib.org/,目前最新版本“6.1.2”,可以下载源码过来学习研究,对应版本的手册地址是https://gmplib.org/gmp-man-6.1.2.pdf,当然是英文版,实在不想看也可以直接跳到附件里早期翻译的版本,本题主要涉及其中的整数运算和数论部分函数。

接下来就是去识别上面的运算函数,将其与gmp库里的函数对应上。本来以为有源码了很好找函数,结果半天也没准确对上,最后还是连蒙带猜的把函数功能调出来,先直接看一下最后对应上来的样子吧:

当看到判断素数时就可以猜到是考察RSA,于是复习相关的数论知识,这里推荐找阮一峰老师的两篇“RSA算法原理”看看,简单易懂。下面简单说一下怎么对应上如上的函数,最简单的方法还是动态调试,去观察上面每个函数的输入输出进行功能判定,再根据参数特征查手册寻找对应的函数。一开始,将输入的两个十六进制大数转化到两个对象里,从第三个参数“16”便可以猜到是表示进制,这样在整数函数里很容易就确定了这个转化函数是“赋值函数”系列,其中第三个参数正好是表示进制数base,第二个参数是我们输入的数串,第一个参数是一个结构体,gmp库里把大数封装在其中,通过动态调试可以观察出它的简单结构,包含一个存储实际数据的地址:
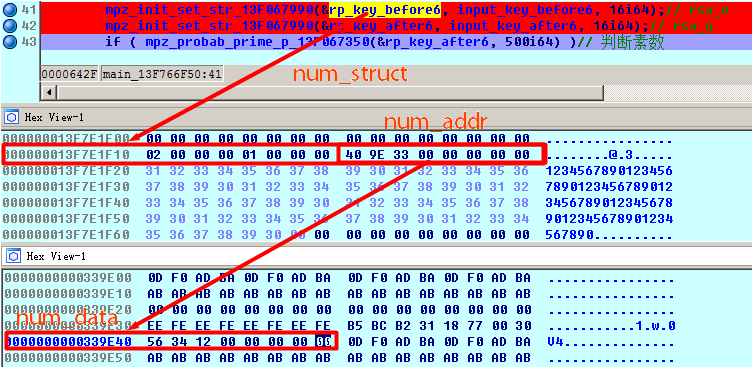
通过该函数,将数串转化为mpz_t结构,后面的运算主要基于该结构,调试过程中可以随时把一个字符串通过该函数转化为此对象,也可以通过该对象的addr字段查看对应的数据内容。接下来的运算可以通过这个特点来控制输入参数,观察输出来判断函数功能,简单的运算都能比较容易对应上函数。比较特殊的函数主要有两个,一个是判断素数的函数mpz_probab_prime_p_13F067350,另一个是求模逆的函数mpz_invert_13F9273B0。第一个函数虽然通过参数类型也能排除掉一些可能性,但是其第三个参数500实在让人有些摸不着头脑。后面一想,输入的两个数有一个数才6位,也可以判断通过,这样的话就表示我们枚举一下6位数就能知道哪些数能通过校验,顺便学习一下IDC脚本,还是贴一段简单暴力的调试代码:
auto buf_rip;
auto buf_rdx;
auto buf_rax;
auto x1, x2, x3, x4, x5, x6;
auto y1, y2, y3, y4, y5, y6;
auto first;
first = 0;
for(x1=0; x1<16; x1++)
{
if(x1 <= 9)
{
y1 = 0x30 + x1;
}
else
{
y1 = 0x41 + x1 - 10;
}
for(x2=0; x2<16; x2++)
{
if(x2 <= 9)
{
y2 = 0x30 + x2;
}
else
{
y2 = 0x41 + x2 - 10;
}
for(x3=0; x3<16; x3++)
{
if(x3 <= 9)
{
y3 = 0x30 + x3;
}
else
{
y3 = 0x41 + x3 - 10;
}
for(x4=0; x4<16; x4++)
{
if(x4 <= 9)
{
y4 = 0x30 + x4;
}
else
{
y4 = 0x41 + x4 - 10;
}
for(x5=0; x5<16; x5++)
{
if(x5 <= 9)
{
y5 = 0x30 + x5;
}
else
{
y5 = 0x41 + x5 - 10;
}
for(x6=0; x6<16; x6++)
{
if(x6 <= 9)
{
y6 = 0x30 + x6;
}
else
{
y6 = 0x41 + x6 - 10;
}
if(first == 0)
{
first = 1;
continue;
}
buf_rip = GetRegValue("RIP");
buf_rip = buf_rip & 0xffffffffffff0000;
SetRegValue(buf_rip + 0x703B, "RIP");
RunTo(buf_rip + 0x704B);
GetDebuggerEvent(WFNE_SUSP, -1);
buf_rdx = GetRegValue("RDX");
PatchByte(buf_rdx + 63, y6);
PatchByte(buf_rdx + 62, y5);
PatchByte(buf_rdx + 61, y4);
PatchByte(buf_rdx + 60, y3);
PatchByte(buf_rdx + 59, y2);
PatchByte(buf_rdx + 58, y1);
RunTo(buf_rip + 0x7061);
GetDebuggerEvent(WFNE_SUSP, -1);
buf_rax = GetRegValue("RAX");
if(buf_rax != 0)Message("sucess!%x%x%x%x%x%x\r\n", y1, y2, y3, y4, y5, y6);
}
}
}
}
}
}
这段代码通过将输入的第二个大数(后64位16进制数0),循环枚举低6位去执行判断函数mpz_probab_prime_p_13F067350,如果返回为1则输出当前枚举数,这样打印出了一系列的满足的判断的数列:
00000B(11)
00000D(13)
000011(17)
000013(19)
000017(23)
00001D(29)
00001F(31)
000025(37)
000029(41)
。。。。。。
显而易见,都是素数(质数)!然后又是质数,又是大数的,很容易就想到是RSA了,对照一下相关的数论知识,下面的运算也就很容易猜出来了。。。
第二个比较难看出来的运算函数是求模逆mpz_invert_13F9273B0,因为运算结果比较难直接看出来(大神忽略不计),不过对照着RSA的算法来看其实也是比较容易猜到的。。。这部分还是请自行对照看看吧,这里就不多说了哈,具体的我在附件的IDB里也标注了。
接着就是理解了算法后去分解程序给的第一个大数即质因数n,这个用RSAtool工具的话比较吃力,不知道要跑多久了,于是果断放弃找在线的分解库:http://factordb.com/ ,把第一个16进制大数转化成10进制后在上面进行查询,果然出来一个破解历史:
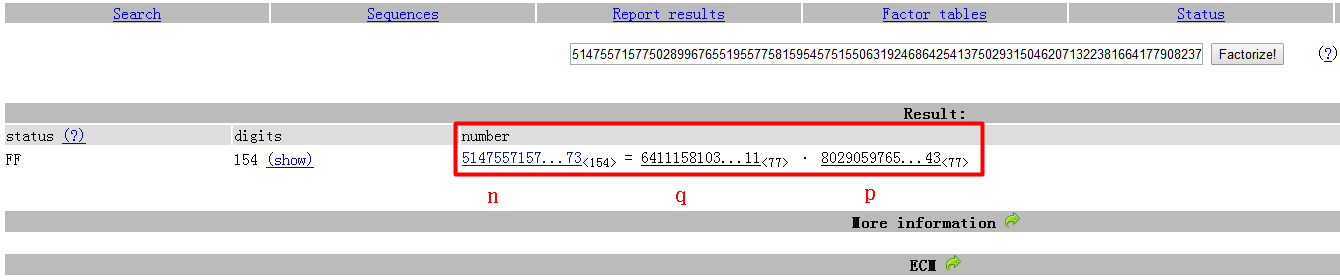
将其转化成16进制后得到一组分解如下,由于程序判断了p和q的大小关系,可以很容易确定q即为我们想要的第二个输入,验证一下可以顺利走到求模逆的流程里:
n = 0x6248BC3AB92A33B000FDB88568F19727F92F79EB68FF6AD73203EFD20A3E331BE941C7AA288095F33BC4B255FD983114D480EFFBEE2E313E6218A57F9CCC8189 = q * p = 0x8DBDDE72E2E693B2AED5C769C0DCB3DA83534480A80E652FFE53544CD91A18C3 * 0xB182DE2AC2DB8735CF01B2AB4CC338C82E2806043302A3CE9EFA861DC36377C3
最后就是求模逆了,也就是我们输入的6位数为e,模逆一下去求d,看是否等于程序给的第二个大数。这样的话也就是第二个大数为d,我们反过来去求e,直接改一下求模逆时的第二个参数e为d(第二个大数)即可在输出的对象里查看求出来的6位数e:
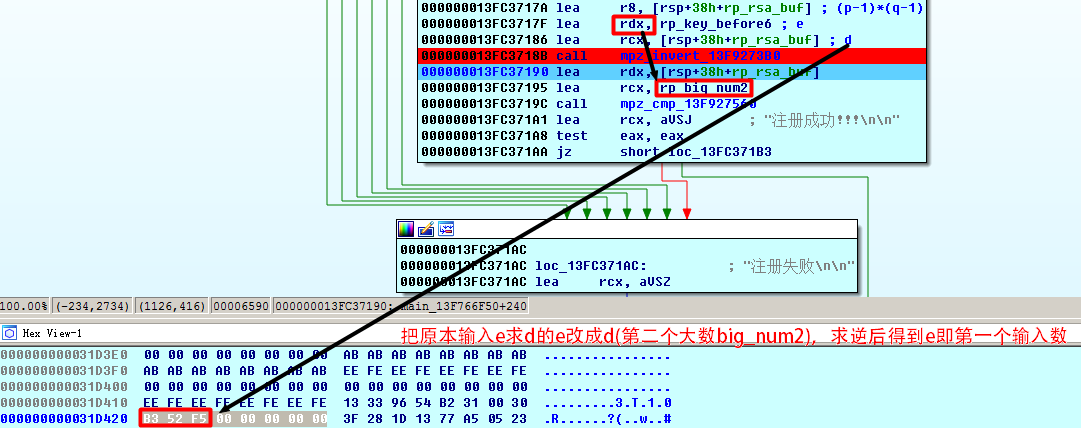
将其作为第一个6位输入数进行验证: