程序运行后，打印“you lose”，题目要求提供一个新文件，使通过程序的验证流程，显示“you win”：

程序验证代码很容易定位，可以通过字符串直接找到函数：

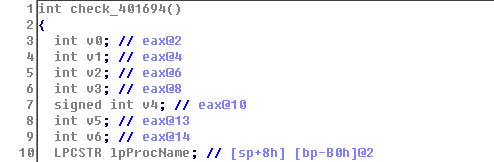
然后发现程序加载了一个不存在的dll文件zapus_dll.dll，应该就是题目要求提供的新文件：

然后获取一个导出函数zapus_get进行调用，看名字应该是取得一些数据，取得的数据输出到输入参数指向的buf里，然后再输入到另一个函数里进行解密，解密完成后进行16字节数据比较，这是第一层验证：

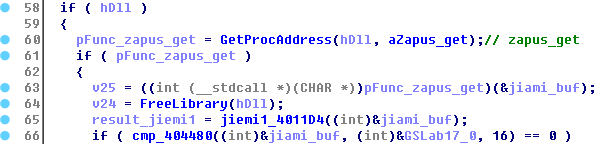
跟进数据解密函数jiemi1_4011D4，解密算法一目了然，不过还是有点小复杂，不是很好理解：

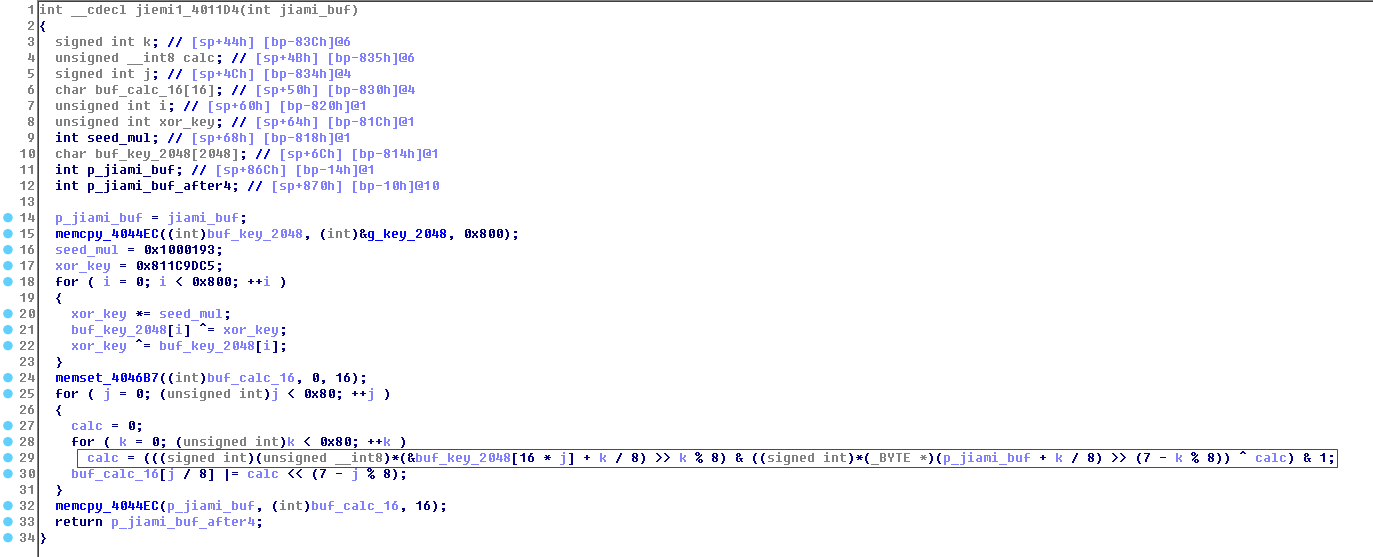
要在dll里面实现对应的加密函数，需要对这个解密算法进行分析逆向，这里简单说一下：

解密函数先用循环的异或和相乘运算生成一个0x800字节的buf_key_2048，这里可以看成是是固定的一些常数数组，下面解密时需要用到。然后解密过程有两层循环，外层循环的含义是进行0x80轮解密，每次获得一个解密数据的比特位进行存储，每8轮存储一个解密数据的字节，存储顺序是从高位到低位，最终正好解密0x10字节的数据。内层循环的含义是进行轮解密，从buf_key_2048数组里按顺序取0x10字节数据，与要解密的0x10字节加密数据一起，按比特位进行相乘和异或累积的运算，运算的结果就是外层循环要存储的一个比特数据。这里也要注意取比特位数据的顺序，buf_key_2048的0x10字节数据时按照从低位到高位的顺序取，而要解密的0x10字节加密数据时按照每个字节从高位到低位的顺序取。

Ok，要实现这个解密函数的逆算法，可以把加密数据的每一位当作一个未知变量，这样这个解密函数的过程就可以看成一个生成线性方程组的过程。百度一下线性方程组的求解，发现是大学线性代数的知识，可以用高斯消元法求解，并且网上也有针对这种二进制异或方程组形式的求解算法。稍微修改一下调整一下各系数的顺序就很容易求出解密函数的逆算法了，以下为dll需要实现的加密算法，完整参见附件：

const int N = 0x100;
int bitsets[N][N];
int n = 0x80;
int m = 0x80;
 
int gauss()
{
    int ans = 0;
    for(int i=0; i<n; i++)
    {
        int p = i;
        while(!bitsets[p][i] && p < m)
        {
            p++;
        }
        if(p >= m)
        {
            return -1;
        }
        ans = max(ans, p);
        if(p != i) 
        {
            for(int j=0; j<=n; j++)
            {
                swap(bitsets[p][j], bitsets[i][j]);
            }
        }
        for(int j=0; j<m; j++)
        {
            if(j != i && bitsets[j][i]) 
            {
                for(int k=0; k<=n; k++)
                {
                    bitsets[j][k] ^= bitsets[i][k];
                }
            }
        }
    }
    return ans;
}
 
char * jiami(char *buf_jiami)    //need to reverse
{
    char *p_key_2048 = get_key_2048();
    memset(g_buf_jiami, 0, 0x10);
    for (int j=0; j<n; j++)
    {
        for (int k=0; k<m; k++)
        {
            bitsets[j][k] = ((signed int)(unsigned __int8)*(&p_key_2048[16 * j] + k / 8) >> k % 8) & 1; //左端序数，从字节低位取
        }
 
        bitsets[j][m] = (buf_jiami[j / 8] & (1 << (7 - j % 8))) >> (7 - j % 8); //右端序数，从字节高位取
    }
    int ans = gauss();
    if(ans == -1)
    {
        return NULL;
    }
    for(int i=0; i<=n; i++)
    {
        g_buf_jiami[i / 8] |= bitsets[i][n] << (7 - i % 8); //求得解，往字节高位存
    }
    return g_buf_jiami;
}

求出逆算法后，在dll里面获取进程PID，并将其将字符串“GSLab17”进行拼接，PID存储在0x10拼接数据的最后一个dword，把拼接数据经过上面实现加密函数，将加密结果在导出函数zapus_get中返回给调用方即可：

bool __stdcall zapus_get(char* buf_jiami)
{    
    char buf_flag[0x10] = {0};
    memcpy(buf_flag, get_flag(), 0x10);
    memcpy(buf_jiami, jiami(buf_flag), 0x10);
    return (memcmp(buf_flag, jiemi(buf_jiami), 0x10) == 0);
}

回到题目程序验证过程，将从dll函数获得的加密字符串通过jiemi1_4011D4解密后，得到的加密前的拼接数据：“GSLab17”+“PID”，与程序事先另外设定好的该串进行比较，则通过第一步验证。

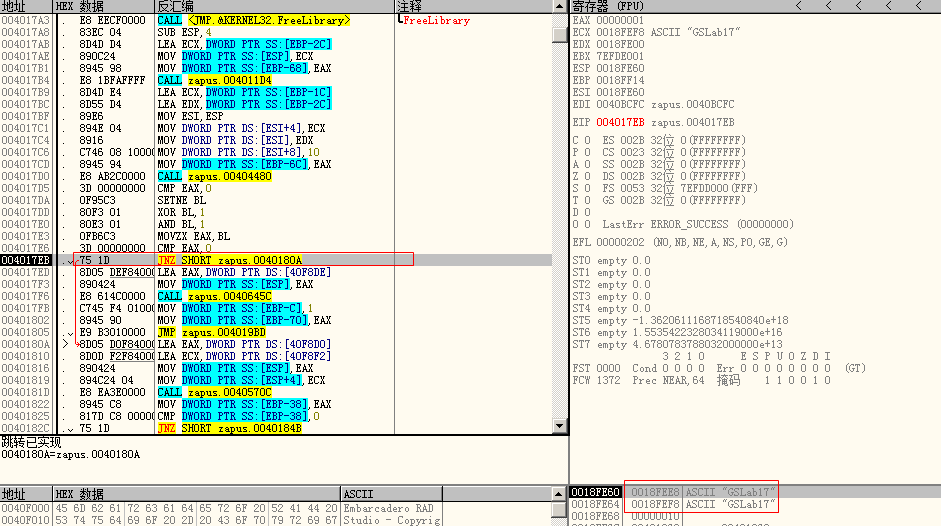
实际上这里有个bug可以利用，仔细观察上图栈区比较数据的两个缓冲区，解密缓冲区地址0018FEE8正好在比较缓冲区地址0018FEF8的相邻低位，而调用zapus_get时没有规定输入参数——解密缓冲区0018FEE8的大小，所以可以直接覆盖到比较缓冲区，控制比较时的数据。不过这种方法可能官方不会承认，因为要求写着新文件必须包含有效的逆算法，权当学习吧。

然后是下一阶段，看到对dll文件再次进行操作，并且函数40570C的参数很像文件打开操作：

跟进去后能发现确实是库函数fopen的实现：

然后跟到函数4058A8基本上就能确认这些库函数的意义以及文件操作的流程：

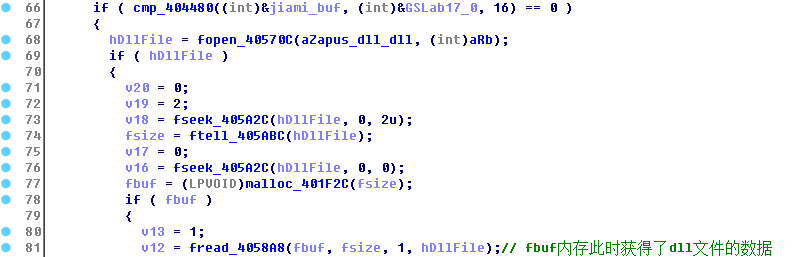
接着是对dll文件数据进行两组计算，每组计算获得一个值，最后要同时等于'aLSG'才能通过：

而这两组计算其实也很简单，是知名算法，第一组是crc32算法，通过sub_401A34初始化表数组的常量即可识别：

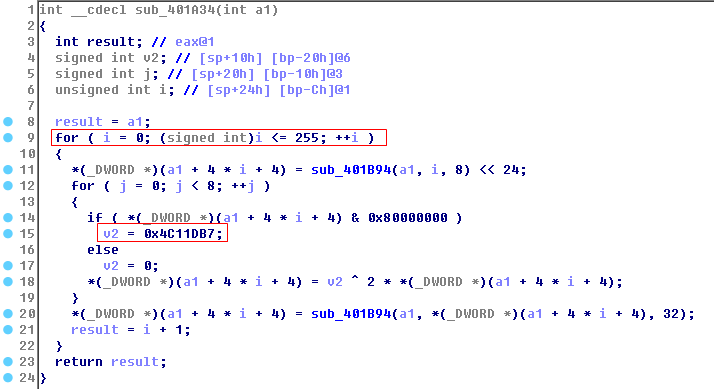
Crc32的主算法在401C10：

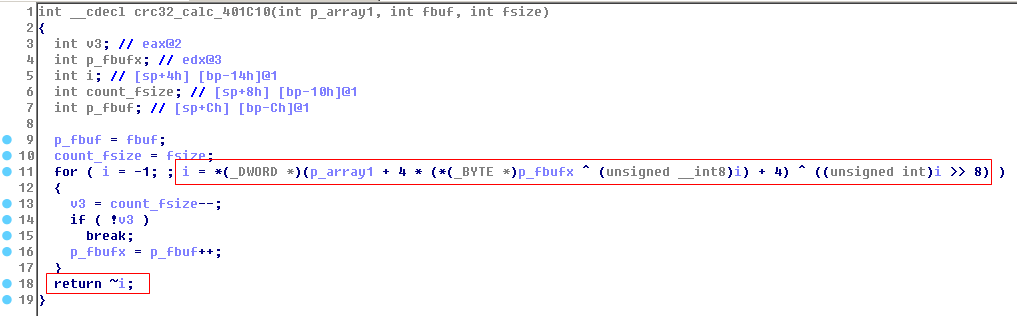
另外一组是fnv哈希算法，同样通过常量可以识别：

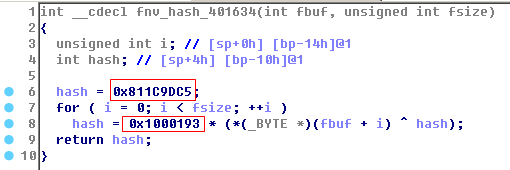
也就是说，这第二步的验证也是最后的验证是要对dll文件同时进行crc32校验和fnv哈希运算，让其同时等于指定的数值：

最直接的思路是类似哈希碰撞的思路，但两种哈希碰撞每种单独碰撞都比较简单，要同时碰撞成一个数却没有那么容易，目前的思路是考虑到两种“哈希”运算的主要操作都是异或、相乘，猜测要和上一步验证一样解线性方程，在文件末尾加入n位数据，数据位设成未知量。未完待续。这一步最后还是没搞定，就学到哪，记到哪吧。

先贴一下一般crc32的实现代码：

unsigned int crc32_table[256];
void init_table()
{
    unsigned int crc;
    for(int i=0; i<256; i++)
    {
        crc = i;
        for(int j=0; j<8; j++)
        {
            if(crc & 1)
            {
                crc = (crc >> 1) ^ 0xEDB88320;
            }
            else
            {
                crc = crc >> 1;
            }
        }
        crc32_table[i] = crc;
    }
}
 
unsigned int crc32(unsigned char *pData, int len, unsigned int seed=0)
{
    unsigned int crc = ~seed;
    init_table();
    for(int i=0; i<len; i++)
    {
        crc = crc32_table[(crc & 0xFF) ^ pData[i]] ^ (crc >> 8);
    }
    return ~crc;
}

Crc算法是数据冗余校验用的，本质上是传输数据对某个选择多项式的模2除法运算，其余数就是附加的crc值，对于标准crc32来说，选择的多项式是X32+X26+X23+X22+X16+X12+X11+X10+X8+X7+X5+X4+X2+X1+1，对应二进制代码：100000100110000010001110110110111即0x104C11DB7。但是一般实现为了追求速度，用空间换时间，先生成一个256的crc表，如上代码所示，然后累积进行异或、选择运算，初始化种子为0（或为已计算数据的crc），最后得到一个校验值。Crc32的校验值为4个字节，所以很容易进行碰撞，找到多对冲突数据。具体可自行参考网上资料。

再看一下fnv哈希的实现代码，具体地说是fnv-1a：

unsigned int fnv_hash(unsigned char *pData, int len, unsigned int seed=0x811C9DC5)
{
    unsigned int hash = seed;
    for (int i=0; i<len; i++)
    {
        hash = 0x1000193 * (pData[i] ^ hash);
    }
    return hash;
}

简单暴力的一个异或累乘，这样由于hash值同样只有4个字节，结果有可能会发生“溢出”，也比较容易进行碰撞。请自行编写碰撞程序吧。

回到题目，要求dll文件的这两种hash值同时等于某个指定的常量，而dll文件是参赛者自行编译的，所以必然有所差异，要构造这么一个特殊的文件，一般是往编译好的dll文件尾部添加一些附加数据来进行碰撞，从这个角度来看，每个参数者实际上是碰撞的初始化“种子数据”不一样而已：

void test_calc_hash()
{
    fstream fs;
    fs.open("zapus_dll.dll", ios::binary | ios::in);
    fs.seekg(0, ios::end);
    int size_file = fs.tellg();
    fs.seekg(0, ios::beg);
    char *pData = new char[size_file];
    fs.read(pData, size_file);
 
    unsigned int crc32_old_file = crc32((unsigned char*)pData, size_file);
    unsigned int fnv_old_file = fnv_hash((unsigned char*)pData, size_file);
 
    char pData_add[] = "weiyiling";
    int size_add = sizeof(pData_add) - 1;
    unsigned int crc32_add = crc32((unsigned char*)pData_add, size_add);
    unsigned int fnv_add = fnv_hash((unsigned char*)pData_add, size_add);
 
    unsigned int crc32_new_file = crc32((unsigned char*)pData_add, size_add, crc32_old_file);
    unsigned int fnv_new_file = fnv_hash((unsigned char*)pData_add, size_add, fnv_old_file);
 
    delete pData;
    fs.close();
}

不过这个题目到这里真不知道怎么继续下去了，个人认为，碰撞能够解出题目的几率实在太小，也懒得尝试，想了几天如何构造线性方程组也没有突破，只好就此作罢。

在看雪上看到@Ericky 牛的帖子，感觉被打脸了，真是瞎了眼，竟然8字节就能碰撞出来，不过能碰撞出来似乎也有它的道理，但是直接穷举64位恐怕不行，就算10亿秒次的速度，也需要18446744073这么多秒才能举得完。而大牛们碰撞的思想，是采用随机数的方法去进行碰撞，看似几率很小，却提高了效率，增加了短时间内能够碰撞出来的机会。。等我也碰出来再贴剩下的代码，看运气。

真正动手去碰撞时才看清，E牛的碰撞一共使用了12个字节的附加数据，其中8个字节随机数据，4个字节用作调整crc使整个新文件crc值满足条件。这样其实是先算crc，然后再碰fnvhash的值。算crc是用的@DonQuixote在看雪上发表的crc32碰撞实现，其中讲解了如何用4个字节数据碰撞指定的任意crc32值。这里先整理搬运过来下面用吧：

unsigned char F(unsigned char x)
{
    return HIBYTE(HIWORD(crc32_table[x]));
}
 
unsigned char G(unsigned char x)
{
    return LOBYTE(HIWORD(crc32_table[x]));
}
 
unsigned char H(unsigned char x)
{
    return HIBYTE(LOWORD(crc32_table[x]));
}
 
unsigned char I(unsigned char x)
{
    return LOBYTE(LOWORD(crc32_table[x]));
}
 
unsigned char RF(unsigned char x)
{
    int i = 0;
    for(i=0; i<=0x0FF;i++)
    {
        if(HIBYTE(HIWORD(crc32_table[i])) == x) 
        {
            break;
        }
    }
    return i;
}
 
unsigned int crc32_crash(unsigned int crc32_old, unsigned int crc32_new)
{
    unsigned char p, o, n, m, a, b, c, d, W, X, Y, Z, A, B, C, D;
 
    crc32_old = ~crc32_old;
    crc32_new = ~crc32_new;
 
    W = HIBYTE(HIWORD(crc32_new));
    X = LOBYTE(HIWORD(crc32_new));
    Y = HIBYTE(LOWORD(crc32_new));
    Z = LOBYTE(LOWORD(crc32_new));
 
    A = HIBYTE(HIWORD(crc32_old));
    B = LOBYTE(HIWORD(crc32_old));
    C = HIBYTE(LOWORD(crc32_old));
    D = LOBYTE(LOWORD(crc32_old));
 
    if (!b_init_table)
    {
        init_table();
    }
 
    p = RF(W);
    o = RF(X^G(p));
    n = RF(Y^G(o)^H(p));
    m = RF(Z^G(n)^H(o)^I(p));
 
    d = m^D;
    c = n^C^I(m);
    b = o^B^H(m)^I(n);
    a = p^A^G(m)^H(n)^I(o);
 
    return MAKELONG(MAKEWORD(d, c), MAKEWORD(b, a));
}

然后也懒得论证什么了，反正没有真正理解牛们讲的生日数原理什么的，直接用上面讲的思路来碰吧，碰到了算运气，我反正也等了挺久才出来，可能真的因为机器渣。先贴碰撞代码，看情况修改自己编译的dll文件的原始crc32和fnvhash值：

void test_calc_hash()
{
    unsigned int crc32_old_file = 0x80eb63d7;
    unsigned int fnv_old_file = 0x0373b33a;
 
    __int64 i = 0;
    const int size_add = 12;
    unsigned char pData_add[size_add] = {0};
 
    __int64 count_try = 0;
    unsigned int crc_add = 0;
    mt19937_64 mt_rand(GetCurrentProcessId());
    while(true)
    {    
        i = mt_rand();
        memcpy(pData_add, &i, 8);
        crc_add = crc32_crash(crc32(pData_add, 8, crc32_old_file), 0x614C5347);
        memcpy(&(pData_add[8]), &crc_add, 4);
        if(fnv_hash(pData_add, size_add, fnv_old_file) == 0x614C5347)
        {
            cout << hex << i << "\t" << hex << crc_add << "\tOK!" << endl;
            break;
        }
        count_try++;
        if (count_try % 100000000 == 0)
        {
            cout << count_try << endl;
        }
    }
}

效率不怎么高，循环一亿次用的时间是分钟级，凑乎碰吧，不行多开几个进程同时进行，估计二十分钟内能出解。。

了却一桩心事吧算是，最后贴个真相。